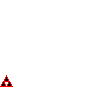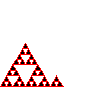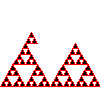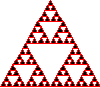Desafio 6
Fractais
são "figuras" curiosas e ao mesmo tempo importantes na
tentativa de entender leis que regem a formação
de coisas aparentemente simples como uma árvore ou uma folha
de samambaia. O estudo de fractais é apaixonante e
há vários programas que permitem
criá-los sem entender nada de
programação (o Gimp
é um programa de imagens que também permite criar
fractais). Mas também podemos simular fractais usando a
linguagem logo.
Um modelo de fractal conhecido como árvorepode
ser construído como a seguir.
 MegaLogo MegaLogo
para
arvore :dist
se :dist < 5 [pare]
pf :dist gd 30
arvore :dist -
10
ge 60
arvore :dist -
10
gd 30 pt :dist
fim
|
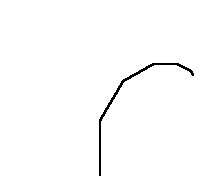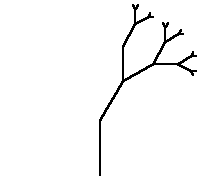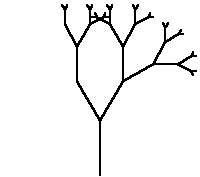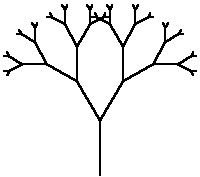
|
   SuperLogo,
xLogo SuperLogo,
xLogo
e MicroMundos
aprenda
arvore :dist
se :dist < 5 [pare]
pf :dist pd 30
arvore :dist -
10
pe 60
arvore :dist -
10
pd 30 pt :dist
fim |
 Imagine Imagine
aprender
arvore :dist
se :dist < 5 [parar]
pf :dist gd 30
arvore :dist -
10
ge 60
arvore :dist -
10
gd 30 pt :dist
fim |
*****
O que o procedimento
faz é basicamente fazer a tartaruga ir para frente e para
trás sucessivas vezes com recursão(o
procedimento arvorechama
o próprio procedimento arvore.
Outro fractal interessante é a peneira de
Sierpinski. Consiste basicamente na
repetição do triângulo de Pascal.
MegaLogo
para
peneira :x :y :lado :nivel
se :nivel = 0 [pentri :x :y :lado pare]
peneira :x :y :lado / 2 :nivel - 1
peneira :x + :lado / 2 :y :lado / 2 :nivel - 1
peneira :x + :lado / 4 :y + :lado * 0.433 :lado / 2 :nivel -
1
fim
|

|
SuperLogo,
MicroMundos e xLogo
aprenda
peneira :x :y :lado :nivel
se :nivel = 0 [pentri :x :y :lado pare]
peneira :x :y :lado / 2 :nivel - 1
peneira :x + :lado / 2 :y :lado / 2 :nivel - 1
peneira :x + :lado / 4 :y + :lado * 0.433 :lado / 2 :nivel -
1
fim |
Imagine
aprender
peneira :x :y :lado
:nivel
se :nivel = 0 [pentri :x :y :lado parar]
peneira :x :y :lado / 2 :nivel - 1
peneira :x + :lado / 2 :y :lado / 2 :nivel - 1
peneira :x + :lado / 4 :y + :lado * 0.433 :lado / 2 :nivel -
1
fim |
MegaLogo
para
pentri :x :y :lado
un
mudex :x mudey :y muderumo 30
ul
repita 3 [pf :lado gd 120]
un
mudex :x + :lado / 2 mudey :y + 2
ul
pinte
fim
|
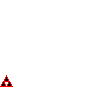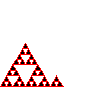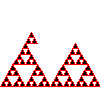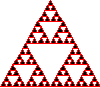
|
SuperLogo,
MicroMundos e xLogo
aprenda
pentri :x :y :lado
un
mudex :x mudey :y mudedç 30
ul
repita 3 [pf :lado pd 120]
un
mudex :x + :lado / 2 mudey :y + 2
ul
pinte
fim |
Imagine
aprender
pentri :x :y
:lado
un
mudarcoorx :x mudarcoory :y
mudarrumo
30 ul repetir 3 [pf :lado gd
120]
un
mudarcoorx :x + :lado / 2 mudarcoory :y + 2
ul preencher
fim |
*****
Como exemplo,
após criar os procedimentos peneira e pentri,
escreva na janela de comandos: peneira 0 0 200 5 e
será desenhado o respectivo fractal de nível 5; peneira
0 0 200 4 e será desenhado o respectivo fractal de
nível 4; e assim por diante.
Outro fractal que chama a
atenção é o da curva de Koch.
MegaLogo
para
fractal :n :lado
verifica
:n = 0 sef [fractal :n - 1 :lado / 3] sev [pf :lado]
ge 60
verifica
:n = 0 sef [fractal :n - 1 :lado / 3] sev [pf :lado]
gd 120
verifica
:n = 0 sef [fractal :n - 1 :lado / 3] sev [pf :lado]
ge 60
verifica
:n = 0 sef [fractal :n - 1 :lado / 3] sev [pf :lado]
fim |

Exemplo: na janela de comandos, escreva fractal
4 50
|
SuperLogo
aprenda
fractal :n :lado
senão
não :n = 0 [ fractal :n - 1 :lado
/ 3 ] [ pf :lado ]
pe 60
senão
não :n = 0 [ fractal :n - 1 :lado
/ 3 ] [ pf :lado ]
pd 120
senão
não :n = 0 [ fractal :n - 1 :lado
/ 3 ] [ pf :lado ]
pe 60
senão
não :n = 0 [ fractal :n - 1 :lado
/ 3 ] [ pf :lado ]
fim |
MicroMundos
aprenda
fractal :n :lado
sesenão
não :n = 0 [ fractal :n - 1
:lado
/ 3] [pf :lado] pe 60
sesenão
não :n = 0 [ fractal :n - 1
:lado
/ 3] [pf :lado] pd 120
sesenão
não :n = 0 [ fractal :n - 1
:lado
/ 3] [pf :lado] pe 60
sesenão
não :n = 0 [ fractal :n - 1
:lado
/ 3] [pf :lado]
fim |
xLogo
aprenda
fractal :n :lado
se
não :n = 0 [ fractal :n - 1 :lado / 3 ] [ pf
:lado ] pe 60
se
não :n = 0 [ fractal :n - 1 :lado / 3 ] [ pf
:lado ] pd 120
se
não :n = 0 [ fractal :n - 1 :lado / 3 ] [ pf
:lado ] pe 60
se
não :n = 0 [ fractal :n - 1 :lado / 3 ] [ pf
:lado ]
fim |
Imagine
aprender
fractal :n :lado
senão
:n = 0 [ pf :lado ] [ fractal :n - 1
:lado / 3 ] ge 60
senão
:n = 0 [ pf
:lado ] [ fractal :n - 1 :lado / 3 ] gd 120
senão
:n = 0 [ pf :lado ] [ fractal :n - 1
:lado / 3 ] ge 60
senão
:n = 0 [ pf
:lado ] [ fractal :n - 1 :lado / 3 ]
fim |
*****
O fractal de Hilbert
é um tanto mais complexo. Abaixo, apresento uma tentativa de
solução. Deve-se escrever na janela de comandos
algo como gerahilbert nível
direção distância, onde
"nível" é o número de
iterações, direção
é o valor 1 ou -1 e distância é um
número que corresponde aos passos da tartaruga.
MegaLogo
para
geraHilbert2 :nivel :direc :dista
se :nivel > 0 [gd -90 * :direc ˜
geraHilbert2 :nivel - 1 -1 * :direc :dista pf :dista / 4 gd
90 * :direc ˜
geraHilbert2 :nivel - 1 :direc :dista pf :dista / 4
˜
geraHilbert2 :nivel - 1 :direc :dista gd 90 * :direc pf
:dista / 4 ˜
geraHilbert2 :nivel - 1 -1 * :direc :dista gd -90 * :direc]
fim |
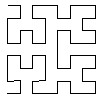
Exemplo: na janela de comandos, escreva geraHilbert2
5 -1 50
|
SuperLogo,
MicroMundos e xLogo
aprenda
geraHilbert2 :nivel :direc :dista
se :nivel>0 [pd -90 * :direc
geraHilbert2 :nivel - 1 (-1) * :direc :dista pf :dista / 4
pd 90 * :direc
geraHilbert2 :nivel - 1 :direc :dista pf :dista / 4
geraHilbert2 :nivel - 1 :direc :dista pd 90 * :direc pf
:dista / 4
geraHilbert2 :nivel - 1 (-1) * :direc :dista pd -90 *
:direc]
fim
|
Imagine
aprender
gerahilbert2 :nivel :direc :dista
se :nivel > 0 [gd -90 * :direc
geraHilbert2 :nivel - 1 -1 * :direc :dista pf :dista / 4 gd
90 * :direc
geraHilbert2 :nivel - 1 :direc :dista pf :dista /
4
geraHilbert2 :nivel - 1 :direc :dista gd 90 * :direc pf
:dista / 4
geraHilbert2 :nivel - 1 -1 * :direc :dista gd -90 * :direc]
fim |
*****
A
curva de Peano (matemático
italiano Giuseppe Peano, 1858-1932) é um fractal que pode
ser conseguido de forma menos complicada que a de Hilbert.
Níveis acima de 6 são bem lentos devido ao
número de iterações envolvidas.
MegaLogo
para
geraPeano :nivel :dista
verifica :nivel = 0
sev [pf :dista]
sef [geraPeano :nivel - 1 :dista / 3 gd -90 ˜
geraPeano :nivel - 1 :dista / 3 gd 90 ˜
geraPeano :nivel - 1 :dista / 3 gd 90 ˜
geraPeano :nivel - 1 :dista / 3 ˜
geraPeano :nivel - 1 :dista / 3 gd 90 ˜
geraPeano :nivel - 1 :dista / 3 gd 90 ˜
geraPeano :nivel - 1 :dista / 3 gd 90 ˜
geraPeano :nivel - 1 :dista / 3 ˜
geraPeano :nivel - 1 :dista / 3]
fim |
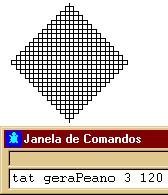
Exemplo: na janela de comandos, escreva
geraPeano 4 390
|
SuperLogo
aprenda
geraPeano :nivel :dista
senão :nivel = 0 [pf :dista] [
geraPeano
:nivel - 1
:dista / 3 pd -90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3
geraPeano :nivel - 1 :dista / 3]
fim |
MicroMundos
aprenda
geraPeano :nivel :dista
sesenão :nivel = 0 [pf :dista] [
geraPeano
:nivel - 1
:dista / 3 pd -90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3
geraPeano :nivel - 1 :dista / 3]
fim
|
xLogo
aprenda
geraPeano :nivel :dista
se :nivel = 0 [pf :dista] [
geraPeano
:nivel - 1 :dista / 3 pd
-90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3 pd 90
geraPeano :nivel - 1 :dista / 3
geraPeano :nivel - 1 :dista / 3]
fim |
Imagine
aprender
gerapeano :nivel :dista
testar :nivel = 0 sev [pf :dista]
sef [geraPeano :nivel - 1 :dista / 3 gd -90
geraPeano :nivel - 1 :dista / 3 gd 90
geraPeano :nivel - 1 :dista / 3 gd 90
geraPeano :nivel - 1 :dista / 3
geraPeano :nivel - 1 :dista / 3 gd 90
geraPeano :nivel - 1 :dista / 3 gd 90
geraPeano :nivel - 1 :dista / 3 gd 90
geraPeano :nivel - 1 :dista / 3
geraPeano :nivel - 1 :dista / 3]
fim |
*****
Uma brincadeira que
pode ser feita com o fractal de Peano é pedir para o logo
fazer repita 8 [pd 45 geraPeano 1 50 geraPeano 2 50 geraPeano
3 50 geraPeano 4 50 pt 200] (no megalogo, substitua pdpor
gd).
Há muitas possibilidades de
variação e aproveitamentos nos procedimentos. Eis
alguns exemplos no xLogo:
|
aprenda pinheiro
ld dt un mudepos [ -20 -150 ] ul
tronco 8 80
mudecordolápis [0 0 0] mudeel 1
fim
aprenda
pinha
mudecordolápis [50 155 50] mudeel 2
pf 10 pe 30 mudeel 1
repita 6 [ pf 10 pt 10 pd 12 ]
mudeel 2 pe 42 pt 10
mudecordolápis [200 125 000]
fim
aprenda tronco :n :d
se :n = 0 [pinha pare]
mudecordolápis [200 125 000]
mudeel 2*:n-1
pf :d pd 45
tronco (:n - 1) :d * 0.7
pe 45 pf :d pe 30
tronco (:n - 1) :d * 0.5
pd 30 pt :d * 2
mudeel 2*:n+1
fim
baseado
em procedimento de Vlado
(http://vlado.fmf.uni-lj.si/educa/logo/ferdos.htm)
|
aprenda
umaarvore :size
se :size < 5 [pare]
pf :size
pe 30 umaarvore :size * (5 + sorteie 5) / 10
pd 60 umaarvore :size * (5 + sorteie 5) / 10
pe 30 pt :size
fim
experimente umaarvore 50
baseado em
procedimento de Clem Rutter
(http://www.rutter.uklinux.net/index2.php?Work:Computing:Logo)
Ou tente esse cenário que criei:
aprenda vai
ld dt un mudex -350 ul
repita 6 [ul umaarvore 40 un mudex 120 + pri pos]
mudepos [250 -20] ul
mudepos [295 20] mudex -350
mudepos [-410 -20] mudex 250
un centro ul mudecl laranja pinte
fim
aprenda umaarvore :size
se :size < 5 [gel pare]
pf :size
pe 30 umaarvore :size * (5 + sorteie 5)/10
pd 60 umaarvore :size * (5 + sorteie 5)/10
pe 30 pt :size
fim
aprenda gel
mudecl escolhe [1 2]
rotule escolhe [* .]
mudecl preto
fim
|
Saiba mais em:
Fractalizando Polígonos
no
SuperLogo. Interessante ideia, adaptei para o
SuperLogo 3.0 (Clique aqui para
obter o código adaptado).
Quantos furos tem uma
peneira? (em
inglês).
Fractais no Ensino
não-Universitário (em
português).
Funções Recursivas.
Fractais (em espanhol). Apresenta aplicativo java para
interagir.
Explorando Recursão e
Fractais(em português).
Turtle Geometry,
por Brian Harvey (em inglês).
No excel: Implementação do
Fractal de Mandelbrot utilizando planilha eletrônica Excel.
 MegaLogo
MegaLogo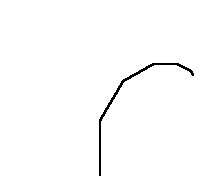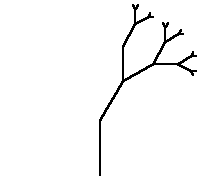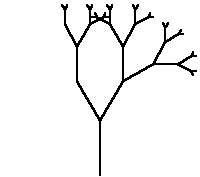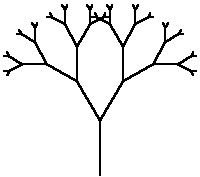


 SuperLogo,
xLogo
SuperLogo,
xLogo Imagine
Imagine