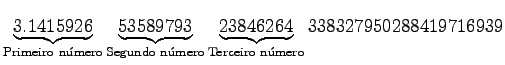Complicando um pouco mais: $\pi$ que gera $\pi$ .....

Como obter um número aleatório? Um número tomado ao sorteie entre 1 e 1 00 0000 é realmente um número aleatório? Apercebe-se muito rapidamente que nossos esforços são apenas uma aproximação do modelo ideal. Bem, é precisamente sobre a maneira de gerar o número aleatório que vamos efetuar algumas mudanças... Não vamos mais utilizar a primitiva sorteie mas usar a seqüência de decimais de $\pi$ . Deixe-me explicar: as decimaies de $\pi$ sempre intrigou os matemáticos pela sua falta de irregularidade, os números de 0 para 9 parecem aparecer em quantidade mais ou menos iguais e de maneira aleatória. Não se pode predizer as próximas casas decimais através das precedentes. Vamos ver a seguir como gerar um número aleatório através das casas decimais de $\pi$ . Em primeiro lugar, deveremos encontrar as primeiras casas decimais de pi (por exemplo, um milhão).

• Existem pequenos programas que o fazem muito bem. Eu aconselho PiFast para Windows e ScnhellPi para Linux.
• Você também pode visitar este endereço e efetuar um "copiar & colar" num arquivo texto:
  http://3.141592653589793238462643383279502884197169399375105820974944592.com/
• Copiar esse arquivo no sítio do xLogo:
  http://xlogo.tuxfamily.org/common/millionpi.txt

Para criar os números aleatórios, pegaremos pacotes de 8 algarismos em seqüência de $\pi$ . Explicação: o arquivo começa assim:
$\underbrace{3.1415926}_{\textrm{Primeiro número}}\underbrace{53589793}_{\textr... ...o número}}\underbrace{23846264}_{\textrm{Terceiro número}}338327950288419716939$ etc
 

Retiro o ponto decimal (. ) do 3.14 ..., que corre o risco de irritar-nos ao extrair as casas decimais. Bem, estando tudo em seu lugar, criamos um novo procedimento chamado sorteiepi e modificamos de leve o procedimento testar

aprenda MDC :a :b
se (resto :a :b)=0 [saída :b][saída MDC :b resto :a :b] 
fim

aprenda testar :tentativas
# Ao abrir um fluxo indicado pelo número 1 para o arquivo millionpi.txt 
# (considere aqui estarmos usando o diretório corrente 
# senão deve-se usar uma lista e um caminho absoluto)
abrafluxo 1 "millionpi.txt
# Guardar na variável "linha" a primeira linha do arquivo millionpi.txt
atr "linha pri leialinha 1
# On initialise la variável contar à 0
atr "contar 0
repita :tentativas [
  se 1=MDC sorteiepi 8 sorteiepi 8  [atr "contar :contar+1]
]
# Calcula a freqüência
atr "f :contar/:tentativas
# Encontrar o valor aproximado de pi
mostre sentença [aproximação de pi:] raizq (6/:f)
fechefluxo 1
fim

aprenda sorteiepi :n
atrlocal "número "
repita :n [
# Se lê plus caracteres sobre a linha
se 0=conte :linha [atr "linha pri leialinha 1]
# Atribui à variável "caractere" o valor do primeiro caractere da linha
atr "caractere pri :linha
# Retira este primeiro caractere da linha.
atr "linha semprimeiro :linha
atr "número pal :número :caractere
]
saída :número
fim
testar 10
aproximação de pi: 2.7386127875258306
testar 100
aproximação de pi: 2.9704426289300225
testar 1000
aproximação de pi: 3.0959109381151797
testar 10000
aproximação de pi: 3.139081837741219

Reencontra-se por conseguinte uma aproximação do número $\pi$ com ajuda de suas próprias casas decimais!!
É ainda possível melhorar este procedimento indicando por exemplo o tempo gasto para o cálculo. Acrescenta-se então na primeira linha do procedimento testar:
atr "inicio tempodec
Acrescenta-se bem na frente de fechefluxo 1:
mostre sentença [Tempo gasto: ] tempodec - :inicio